- MST : Minimum Spanning Tree
- 그래프 상의 모든 노드들을 최소 비용으로 연결하는 방법 : 크루스칼, 프림
노드와 간선정보가 주어졌을 때 최소가 되게 노드들을 한 번만 연결하는 방법
MST 관련 문제들은 내부 알고리즘은 동일. 문제 파악한 후 MST 형태인 것만 떠올면 풀 수 있음
- 크루스칼 (Kruskal) 알고리즘
· 간선 중 최소 값을 가진 간선부터 연결
· 사이클 발생 시 다른 간선 선택
· 주로 간선 수가 적을 때 사용
· O(Elog E)
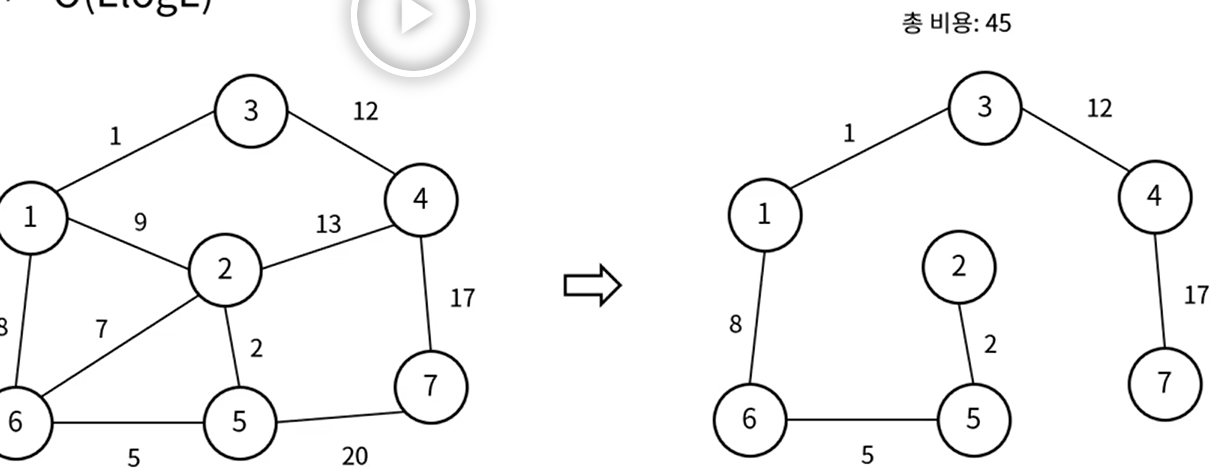
- 간선 정보들을 오름차순 Sorting 작업 필요
- 사이클 발생 체크하는 Union-Find 테이블
초기 : 각 자기 자신으로 초기화

1. 처음에 가장 작은 가중치인 1을 선택해서 1 - 3 노드를 연결하면 3의 부모노드는 연결된, 자기자신보다 더 작은 숫자인 1로 업데이트 -> 부모노드가 같은 것 끼리 연결돼있음을 알려줌.
2. 그다음 작은 가중치인 2를 선택, 2 - 5 연결. 5의 부모노드를 2로 업데이트
3. 다음 가중치 5 선택. 5 - 6 연결 6의 부모노드는 5가 가진 부모노드값 2로 업데이트
4. 가중치 7 선택 2 - 6 연결하면 6의 부모노드는 이미 2였으므로 이미 연결된 애들임을 알 수 있음.-> 사이클 발생 연결X
5. 가중치 8. 6 -1 연결하면 6의 부모노드와 6과 같은 부모노드를 가지는 5, 2노드의 부모노드를 모두 1로 업데이트
6. 가중치 9. 1 -2 연결하면 이미 2의 부모노드가 1이므로 사이클 발생. 연결 X
7. 가중치 12. 3 - 4 연결후 4의 부모노드를 3의 부모노드인 1로 업데이트
8. 가중치 13. 2 - 4 연결하면 부모노드가 1로 같으므로 사이클 발생 연결X
9. 가중치 17. 4 - 7 연결하고 7의 부모노드 1로 업데이트
10. 가중치 20. 5 - 7 연결하면 둘의 부모노드가 1로 같으므로 사이클 발생. 연결 X
Union-Find의 모든 부모노드가 1로 변경되면서 연결이 되었음을 확인.
- 프림 (prim) 알고리즘
· 임의의 노드에서 시작
· 연결된 노드들의 간선 중 낮은 가중치를 갖는 간선 선택
· 간선의 갯수가 많을 때 크루스칼 보다 유리
· O(Elog V) -> Priority Queue를 이용했을 때
초기 : 방문 여부를 알려줄 visited 배열을 모두 0으로 초기화

간선 sorting할 필요 X 따라서 간선의 갯수가 많을 때 크루스칼 보다 유리
1. 임의의 노드 1번 선택 1의 visited 1로 업데이트
2. 1과 연결된 간선 중 가장 낮은 1을 선택. 3의 visited 1로 업데이트
3. 이제 연결된 간선 중에서는 8, 9, 12가 있음 그 중 가장 작은 8 선택. 6의 visited 1로 업데이트
4. 연결된 간선은 7,5,9,12가 있음. 그 중 가장 작은 5 선택. 5의 visited 1로 업데이트
5. 연결된 간선 : 2,12,20 중 가장 작은 2 선택. 2의 visited 1로 업데이트
6. 연결된 간선 : 7,9,12,13중 가장 작은 7 선택시 6이 이미 방문했으므로 그다음 9선택. 1도 방문했으므로 그다음 12선택. 4의 visited를 1로 업데이트.
7. 연결된 간선 : 13, 17 중 13은 2를 이미 방문했으므로 17선택. 7의 visited를 1로 바꿈.
<크루스칼 알고리즘 구현>
// 알고리즘 - 최소 신장 트리
// 크루스칼 알고리즘
import java.util.Arrays;
public class Practice {
static int parents[]; //Union-Find를 위한 배열
public static int kruskal(int[][] data, int v, int e) {
int weightSum = 0;
Arrays.sort(data, (x, y) -> x[2] - y[2]); //간선을 기준으로 오름차순 sorting
parents = new int[v + 1];
for (int i = 1; i < v + 1; i++) {
parents[i] = i; //각각의 위치에 자기자신으로 초기화
}
for (int i = 0; i < e ; i++) {
if (find(data[i][0]) != find(data[i][1])) { //서로 연결이 되어있지 않은 케이스
union(data[i][0], data[i][1]);
weightSum += data[i][2];
}
System.out.println(Arrays.toString(parents));
}
return weightSum;
}
public static void union (int a, int b) { //연결이 되었을 때 두 개의 노드를 같은 집합으로 묶어줌.
int aP = find(a);
int bP = find(b);
if (aP != bP) {
parents[aP] = bP;
}
}
public static int find(int a) { //a라는 노드가 최종적으로 어디 연결되어있는지 찾아주는 메소드
if (a == parents[a]) {
return a;
}
return parents[a] = find(parents[a]); //사이클 체크를 위해 부모노드의 같은 부모로 계속해서 업데이트 해주는 부분
}
public static void main(String[] args) {
// Test code
int v = 7;
int e = 10;
int[][] graph = {{1, 3, 1}, {1, 2, 9}, {1, 6, 8}, {2, 4, 13}, {2, 5, 2}, {2, 6, 7}, {3, 4, 12}, {4, 7, 17}, {5, 6, 5}, {5, 7, 20}};
System.out.println(kruskal(graph, v, e));
}
}근데 이렇게 하면 결과는 잘 나오지만 이론처럼 모든 Parents 값이 1로 맞춰지지 않는다.
Union 메소드에서 parents[bP] = aP로 바꿔주니까 됐다.
사이클 체크만 하면 돼서 의미 없나 ?
<프림 알고리즘 구현>
우선순위 큐, visited 배열 사용
// 프림 알고리즘
import java.sql.Array;
import java.util.ArrayList;
import java.util.PriorityQueue;
public class Practice {
static class Node {
int to;
int weight;
public Node(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
public static int prim(int [][]data, int v, int e) {
int weightSum = 0;
ArrayList <ArrayList<Node>> graph = new ArrayList<>();
for (int i = 0; i < v + 1; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < e; i++) { //간선 정보 양방향 연결
graph.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
graph.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
}
boolean[] visited = new boolean[v + 1];
PriorityQueue <Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.offer(new Node(1, 0));
int cnt = 0;
while (!pq.isEmpty()) {
Node cur = pq.poll();
cnt += 1;
if (visited[cur.to]) {
continue;
}
visited[cur.to] = true;
weightSum += cur.weight;
if (cnt == v) {
return weightSum;
}
for (int i = 0; i < graph.get(cur.to).size(); i++) {
Node adjNode = graph.get(cur.to).get(i);
if (visited[adjNode.to]) {
continue;
}
pq.offer(adjNode);
}
}
return weightSum;
}
public static void main(String[] args) {
// Test code
int v = 7;
int e = 10;
int[][] graph = {{1, 3, 1}, {1, 2, 9}, {1, 6, 8}, {2, 4, 13}, {2, 5, 2}, {2, 6, 7}, {3, 4, 12}, {4, 7, 17}, {5, 6, 5}, {5, 7, 20}};
System.out.println(prim(graph, v, e));
}
}Practice 1)
// 이 행성 간을 빨리 오가기 위해 새롭게 터널을 구축하려 한다.
// 행성은 (x, y, z) 좌표로 주어진다.
// 행성1: (x1, y1, z1), 행성2: (x2, y2, z2)
// 이 때 행성간 터널 연결 비용은 min(|x1-x2|, |y1-y2|, |z1-z2|) 로 계산한다.
// n 개의 행성 사이를 n-1 개의 터널로 연결하는데 드는 최소 비용을 구하는 프로그램을 작성하세요.
// 입출력 예시
// 입력:
// data = {{11, -15, -15}, {14, -5, -15}, {-1, -1, -5}, {10, -4, -1}, {19, -4, 19}}
// 출력: 4
* n 개를 n -1 개로 연결한다는게 MST고 최소비용까지 나왔으니 명확해짐.
- Point클래스 : 행성 x, y, z값 관리
- Edge클래스 : 행성간의 간선 정보 관리
- 각각 x축, y축 z축 기준으로 정렬하고 순차적으로 요소값의 차이가 weight가 되어 edges 리스트에 모두 모음.
- 모은 edges 리스트를 기준으로 kruskal 메소드를 통해 행성과 행성을 연결하는데 최소 비용을 구함.
와 ! 갑자기 좀 깨달음을 얻었다.
x, y, z 축간 모든 행성들의 가중치를 edges배열에 저장, Edge는 weight기준 오름차순 정렬
kruskal에서 가중치 제일 작은 것 부터 연결시켜주는데 추후에 다른 축 값이 나온다고해도 앞에서 나온 더 작은 가중치 값에 의해 이미 행성들이 연결이 되어있으므로 또 연결하지 않음 !
// Practice1
// 2250년, 인류는 지구 뿐 아니라 여러 행성을 다니며 살고 있다.
// 이 행성 간을 빨리 오가기 위해 새롭게 터널을 구축하려 한다.
// 행성은 (x, y, z) 좌표로 주어진다.
// 행성1: (x1, y1, z1), 행성2: (x2, y2, z2)
// 이 때 행성간 터널 연결 비용은 min(|x1-x2|, |y1-y2|, |z1-z2|) 로 계산한다.
// n 개의 행성 사이를 n-1 개의 터널로 연결하는데 드는 최소 비용을 구하는 프로그램을 작성하세요.
// 입출력 예시
// 입력:
// data = {{11, -15, -15}, {14, -5, -15}, {-1, -1, -5}, {10, -4, -1}, {19, -4, 19}}
// 출력: 4
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
public class Practice {
static class Point {
int idx;
int x;
int y;
int z;
public Point(int idx, int x, int y, int z) {
this.idx = idx;
this.x = x;
this.y = y;
this.z = z;
}
}
static class Edge implements Comparable<Edge>{
int from;
int to;
int weight;
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return this.weight - o.weight;
}
}
static int parents[]; //Union-find를 위한 배열
static ArrayList<Edge> edges;
public static int solution(int[][] data) {
int n = data.length; //행성 갯수
Point []points = new Point[n]; //n개의 행성 좌표 관리 배열
for (int i = 0; i < n; i++) {
points[i] = new Point(i, data[i][0], data[i][1], data[i][2]);
}
edges = new ArrayList<>();
//크루스칼 이용할 건데 각 축 값의 최솟값을 구해야하니까
//x축, y축, z축 기준 간선을 모두 모아서 크루스칼 적용 -> 이 문제의 응용점
//x축 기준 간선 추가
Arrays.sort(points, (p1, p2) -> p1.x - p2.x);
for (int i = 0; i < n - 1; i++) {
int weight = Math.abs(points[i].x - points[i + 1].x);
edges.add(new Edge(points[i].idx, points[i + 1].idx, weight));
}
//y축 기준 간선 추가
Arrays.sort(points, (p1, p2) -> p1.y - p2.y);
for (int i = 0; i < n - 1; i++) {
int weight = Math.abs(points[i].y - points[i + 1].y);
edges.add(new Edge(points[i].idx, points[i + 1].idx, weight));
}
//z축 기준 간선 추가
Arrays.sort(points, (p1, p2) -> p1.z - p2.z);
for (int i = 0; i < n - 1; i++) {
int weight = Math.abs(points[i].z - points[i + 1].z);
edges.add(new Edge(points[i].idx, points[i + 1].idx, weight));
}
for (Edge i : edges) {
System.out.println(i.from+" "+i.to+" "+i.weight);
}
Collections.sort(edges); //weight값 기준 오름차순 정렬
System.out.println("정렬 후");
for (Edge i : edges) {
System.out.println(i.from+" "+i.to+" "+i.weight);
}
//kruskal
return kruskal(n, edges);
}
public static int kruskal(int n, ArrayList <Edge>edges) {
parents = new int[n];
for (int i = 0; i < n; i++) {
parents[i] = i; //자기자신으로 초기화
}
int weightSum = 0;
for (int i = 0; i < edges.size(); i++) {
Edge edge = edges.get(i);
if (find(edge.to) != find(edge.from)) {
union(edge.to, edge.from);
weightSum += edge.weight;
}
}
return weightSum;
}
public static void union(int a, int b) {
int aP = find(a);
int bP = find(b);
if (aP != bP) {
parents[aP] = bP;
}
}
public static int find(int a) {
if (a == parents[a]) {
return a;
}
return parents[a] = find(parents[a]);
}
public static void main(String[] args) {
// Test code
int[][] data = {{11, -15, -15}, {14, -5, -15}, {-1, -1, -5}, {10, -4, -1}, {19, -4, 19}};
System.out.println(solution(data));
}
}Practice 2)
// 도로는 양방향이고 연결된 도로는 유지하는데 비용이 든다.
// 새롭게 도시 계획을 개편하며 기존의 도시를 두 개의 도시로 분할해서 관리하고자 한다.
// 도시에는 하나 이상의 건물이 있어야 하고,
// 도시 내의 임의의 두 건물은 도로를 통해 이동 가능해야 한다.
// 두 건물 간 도로가 직접 연결이 되지 않고 다른 건물을 통해서 이동해도 가능하다.
// 새롭게 개편하는 도시 계획에 따라 구성했을 때 최소한의 도로 유지비 비용 계산 프로그램을 작성하세요.
// 입출력 예시
// 입력:
// v: 7
// e: 12
// data: {{1, 2, 3}, {1, 3, 2}, {1, 6, 2}, {2, 5, 2},
// {3, 2, 1}, {3, 4, 4}, {4, 5, 3}, {5, 1, 5},
// {6, 4, 1}, {6, 5, 3}, {6, 7, 4}, {7, 3, 6}}
// 출력: 8
* 두 건물간 도로가 직접 연결이 되지 않고 다른 건물을 통해서 이동 가능 -> 여기까지만 읽어도 MST
도로들을 최소한의 비용으로 다 이은다음 가장 큰 비용을 끊어주면 됨.
// Practice2
// V 개의 건물과 E 개의 도로로 구성된 도시가 있다.
// 도로는 양방향이고 연결된 도로는 유지하는데 비용이 든다.
// 새롭게 도시 계획을 개편하며 기존의 도시를 두 개의 도시로 분할해서 관리하고자 한다.
// 도시에는 하나 이상의 건물이 있어야 하고,
// 도시 내의 임의의 두 건물은 도로를 통해 이동 가능해야 한다.
// 두 건물 간 도로가 직접 연결이 되지 않고 다른 건물을 통해서 이동해도 가능하다.
// 새롭게 개편하는 도시 계획에 따라 구성했을 때 최소한의 도로 유지비 비용 계산 프로그램을 작성하세요.
// 입출력 예시
// 입력:
// v: 7
// e: 12
// data: {{1, 2, 3}, {1, 3, 2}, {1, 6, 2}, {2, 5, 2},
// {3, 2, 1}, {3, 4, 4}, {4, 5, 3}, {5, 1, 5},
// {6, 4, 1}, {6, 5, 3}, {6, 7, 4}, {7, 3, 6}}
// 출력: 8
import java.util.ArrayList;
import java.util.PriorityQueue;
public class Practice {
static class Node {
int to;
int weight;
public Node(int to,int weight) {
this.to = to;
this.weight = weight;
}
}
static ArrayList <ArrayList<Node>> graph;
static boolean []visited;
public static void solution(int v, int e, int[][] data) {
graph = new ArrayList<>();
for (int i = 0; i < v + 1; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < e; i++) {
graph.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
graph.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
}
visited = new boolean[v + 1];
System.out.println(prim());
}
public static int prim() {
PriorityQueue <Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.offer(new Node(1, 0));
int weightSum = 0;
int max = Integer.MIN_VALUE;
while (!pq.isEmpty()) {
Node cur = pq.poll();
if (visited[cur.to]) {
continue;
}
visited[cur.to] = true;
weightSum += cur.weight;
max = Math.max(max, cur.weight);
for (int i = 0; i < graph.get(cur.to).size() ; i++) {
Node adjNode = graph.get(cur.to).get(i);
if (visited[adjNode.to] == true) {
continue;
}
pq.offer(adjNode);
}
}
return weightSum - max;
}
public static void main(String[] args) {
// Test code
int v = 7;
int e = 12;
int[][] data = {{1, 2, 3}, {1, 3, 2}, {1, 6, 2}, {2, 5, 2},
{3, 2, 1}, {3, 4, 4}, {4, 5, 3}, {5, 1, 5},
{6, 4, 1}, {6, 5, 3}, {6, 7, 4}, {7, 3, 6}};
solution(v, e, data);
}
}어떻게 edge리스트를 구성할지가 관건같다.
'알고리즘 > 개념' 카테고리의 다른 글
| 5주차 알고리즘 복습 - 다이나믹 프로그래밍 (0) | 2023.08.06 |
|---|---|
| 5주차 알고리즘 복습 - 그리디 (0) | 2023.08.06 |
| 5주차 알고리즘 복습 - 투 포인터 (0) | 2023.08.06 |
